Integer Base Converter |
| この情報はストアのものより古い可能性がございます。 | ||||
| 価格 | 120円 | ダウンロード |
||
|---|---|---|---|---|
| ジャンル | 教育 | |||
サイズ | 480.0KB | |||
| 開発者 | Chris Pappas | |||
| 順位 |
| |||
| リリース日 | 2014-04-02 01:47:28 | 評価 | 評価が取得できませんでした。 | |
| 互換性 | iOS 7.1以降が必要です。 iPhone、iPad および iPod touch 対応。 | |||
Numeric Bases
Many would argue that the birth of the computer age took place in Bletchley Park during World War II. Alan Turing guided much of this work using an early form of a hand crafted vacuum tube computer. The goal of Bletchley Park scientists and engineers was to break the German enigma codes.
The vacuum tubes of that era were the predecessors of the transistors and integrated circuits we use today. They didn’t operate as amplifiers, but as switches turning currents on and off. This on and off action translated to voltage levels that represented on and off, true and false, and logic 1 and 0. One single wire, operating from such an output represents a single data bit. When multiple bits are used to transmit data, the multiple wires are called a data bus. Early PC and Mac® computers had 8-bit data busses (eight wires). Today, most personal computers use 64-bit data busses (sixty-four wires).
Binary arithmetic is the native language of the computer, while humans are most comfortable with decimal arithmetic. Translating from a binary base, or radix, to a decimal base and back is a fundamental exercise for most computer science students. Intermediate bases such as hexadecimal and octal have also been popular. The octal base, or base 8, was favored by many IBM® programmers during the 1960’s but is seldom used today. The hexadecimal base, or base 16, has become more popular because of the easy translation back and forth to binary. Hexadecimal notation is easier and shorter to write than long strings of 1’s and 0’s.
If you have programmed with assembly language or perhaps C/C++, then you are familiar with the need to convert from one base to another, specifically binary, hexadecimal and decimal.
Base 16, or hexadecimal, uses the digits 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E and F
Base 10, or decimal, uses the digits 0,1,2,3,4,5,6,7,8 and 9
Base 2, or binary, uses the digits 0 and 1
Integer number conversions from one base to another are encountered 99% of the time, due to the fact that the least-significant bit on any data bus is either a 1 or a 0. There are no fractional values on a computer’s data bus. This simply means that only integers are sent across the data bus, and if you want to transmit “real” number values with fractional or decimal components other means must be employed. The “other means” typically requires that real numbers be encoded to appear as integers. (for more information on this topic, see the IEEE 754 conversion standards).
Since most modern data busses are 64-bits in size, most base converters should perform this size conversion accurately. For hexadecimal numbers, a 64-bit data bus provides a range of positive values from:
0 to FFFFFFFFFFFFFFFF
For decimal numbers, this bus provides a range of positive values from:
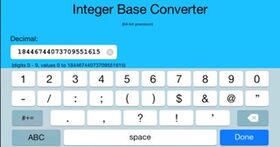
0 to 18446744073709551615
Finally, for binary numbers, this range of positive integers is from:
0 to 1111111111111111111111111111111111111111111111111111111111111111
The maximum values represented by a 64-bit data bus could easily hold the estimated count of the number of stars in our galaxy (approximately 300 billion) but falls short of holding the total estimated number of stars in the universe (1 septillion). Is there a need for a larger data bus? Only time will tell!
However, if you want the hexadecimal and binary equivalents of 300 billion stars, well, our base converter is ready to provide those results easily and accurately.
Many would argue that the birth of the computer age took place in Bletchley Park during World War II. Alan Turing guided much of this work using an early form of a hand crafted vacuum tube computer. The goal of Bletchley Park scientists and engineers was to break the German enigma codes.
The vacuum tubes of that era were the predecessors of the transistors and integrated circuits we use today. They didn’t operate as amplifiers, but as switches turning currents on and off. This on and off action translated to voltage levels that represented on and off, true and false, and logic 1 and 0. One single wire, operating from such an output represents a single data bit. When multiple bits are used to transmit data, the multiple wires are called a data bus. Early PC and Mac® computers had 8-bit data busses (eight wires). Today, most personal computers use 64-bit data busses (sixty-four wires).
Binary arithmetic is the native language of the computer, while humans are most comfortable with decimal arithmetic. Translating from a binary base, or radix, to a decimal base and back is a fundamental exercise for most computer science students. Intermediate bases such as hexadecimal and octal have also been popular. The octal base, or base 8, was favored by many IBM® programmers during the 1960’s but is seldom used today. The hexadecimal base, or base 16, has become more popular because of the easy translation back and forth to binary. Hexadecimal notation is easier and shorter to write than long strings of 1’s and 0’s.
If you have programmed with assembly language or perhaps C/C++, then you are familiar with the need to convert from one base to another, specifically binary, hexadecimal and decimal.
Base 16, or hexadecimal, uses the digits 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E and F
Base 10, or decimal, uses the digits 0,1,2,3,4,5,6,7,8 and 9
Base 2, or binary, uses the digits 0 and 1
Integer number conversions from one base to another are encountered 99% of the time, due to the fact that the least-significant bit on any data bus is either a 1 or a 0. There are no fractional values on a computer’s data bus. This simply means that only integers are sent across the data bus, and if you want to transmit “real” number values with fractional or decimal components other means must be employed. The “other means” typically requires that real numbers be encoded to appear as integers. (for more information on this topic, see the IEEE 754 conversion standards).
Since most modern data busses are 64-bits in size, most base converters should perform this size conversion accurately. For hexadecimal numbers, a 64-bit data bus provides a range of positive values from:
0 to FFFFFFFFFFFFFFFF
For decimal numbers, this bus provides a range of positive values from:
0 to 18446744073709551615
Finally, for binary numbers, this range of positive integers is from:
0 to 1111111111111111111111111111111111111111111111111111111111111111
The maximum values represented by a 64-bit data bus could easily hold the estimated count of the number of stars in our galaxy (approximately 300 billion) but falls short of holding the total estimated number of stars in the universe (1 septillion). Is there a need for a larger data bus? Only time will tell!
However, if you want the hexadecimal and binary equivalents of 300 billion stars, well, our base converter is ready to provide those results easily and accurately.
ブログパーツ第二弾を公開しました!ホームページでアプリの順位・価格・周辺ランキングをご紹介頂けます。
ブログパーツ第2弾!
アプリの周辺ランキングを表示するブログパーツです。価格・順位共に自動で最新情報に更新されるのでアプリの状態チェックにも最適です。
ランキング圏外の場合でも周辺ランキングの代わりに説明文を表示にするので安心です。
サンプルが気に入りましたら、下に表示されたHTMLタグをそのままページに貼り付けることでご利用頂けます。ただし、一般公開されているページでご使用頂かないと表示されませんのでご注意ください。
幅200px版
幅320px版
Now Loading...

「iPhone & iPad アプリランキング」は、最新かつ詳細なアプリ情報をご紹介しているサイトです。
お探しのアプリに出会えるように様々な切り口でページをご用意しております。
「メニュー」よりぜひアプリ探しにお役立て下さい。
Presents by $$308413110 スマホからのアクセスにはQRコードをご活用ください。 →
Now loading...